第一コラムラボ

このたびは，第一学習社 Column Lab.（コラムラボ）に，アクセスいただきありがとうございます。コラムラボは，身の回りの事柄や最新のニュースをコンテンツ化して，学びへの探究心をくすぐるコラム教材を掲載する第一学習社のWebメディアです。

【数学】神秘的な素数の世界＜後編＞

数学

f:id:digitalmedia-d1g:20221122132832j:plain

前編では，ウラムの螺旋やメルセンヌ素数の紹介，そして素数が無数に存在することの証明を行いました。

後編では素数の判定方法や素数定理など，より踏み込んだ内容に触れていきます。

素数を見つける
- エラトステネスの篩
- ウィルソンの定理
素数を求める式!?
- オイラーの素数生成多項式
素数を数える
- 素数定理
まとめ
- 参考書籍

素数を見つける

素数は不規則に現れますが，数が大きくなるにつれて，素数かどうかを判定するのは難しくなっていきます。

エラトステネスの篩

ある整数以下のすべての素数を発見するには，一般的にエラトステネスの篩ふるい （素数を残しながら，その素数の倍数を順に消していく方法）という，原始的ですが効率的な方法が使われます。

この方法で調べると，100までの素数を25個探すことができました。^※

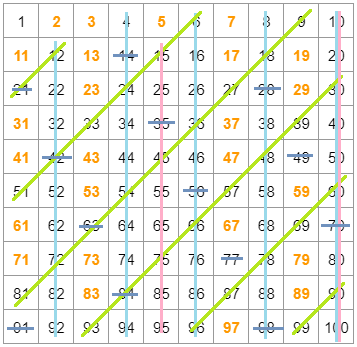
エラトステネスの篩 — エラトステネスの篩を使い，100までの素数を求めよう

※100の平方根は10なので、素数7の倍数を消した時点で操作を終了してよい。

しかし，桁数が大きくなると，たとえコンピュータを使ったとしても素数かどうかを判定するのは困難になります。

この素数の見分けにくさを「鍵」として，クレジットカードの入力などの暗号化（RSA暗号）に使われています。私たちが便利に買い物できるのは，素数のおかげといっても過言ではありません。

ウィルソンの定理

ある数が素数かどうかを判定するには，ウィルソンの定理という方法もあります。

ウィルソンの定理

2以上の整数 $p$ について， $p$ が素数 $\Leftrightarrow$ $(p-1)!\equiv -1　(mod p)$

つまり， $1$ から $p-1$ までを掛けて $p$ で割ったとき，余りが $p-1$ になれば $p$ は素数です。

ただし， $p$ が大きくなるにつれて，とてつもない計算量になるため，あまり実用的とは言えません。

例） $7$ が素数かどうかを判定したい。
　　 $(7-1)!=720$
　　 $720\equiv 6(mod 7)$ より $7$ は素数である。

素数を求める式!?

ある数が素数かどうか判定するのが難しければ，そもそも素数を生み出す式はないのでしょうか。

実は，ウィルソンの定理やガウス記号^※を用いて，n番目の素数をアルゴリズム的に表すことができる式などが知られています。

ただし，nを代入すると直接的にn番目の素数が求められるような式は未だに発見されておらず，素数が出現する規則性がわかったわけではありません。

※ガウス記号 []：その数を超えない最大の整数を表す記号。 $\lfloor x \rfloor$ と書かれることもあり，これを床関数という。

「素数に一般項はない！」
と主張する人をまれに見かけますが、それは嘘です。
画像の式に好きな整数nを代入すると、n番目の素数が得られます。 pic.twitter.com/GF6hCJDVuF
— 数学を愛する会 (@mathlava) 2021年6月6日

mathworld.wolfram.com

オイラーの素数生成多項式

ところで，"一部の"素数を生み出す式はいくつも発見されています。スイスの数学者レオンハルト・オイラー（1707~1783）は，素数を続けて生み出す式を数多く考えました。その一つが以下の二次式です。

オイラーの素数生成多項式（ $p=41$ ）

$f(n)=n^2+n+41$

なんと， $n$ に0から39を順に代入すると連続して40個の素数が出てきます。実際に代入してみると，確かにすべて素数であることが確認できます。

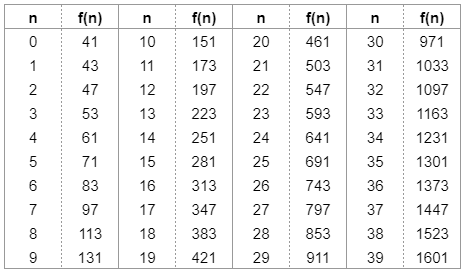
オイラーの素数生成多項式 — 0から39を代入していくと…

「君，今すぐ素数を40個言いなさい！」と上司に脅されても，この多項式を覚えていれば慌てることはありませんね。

$n$ が40以上になると素数でない数も現れますが，驚くことにこの多項式は， $n=40$ より先でも高い割合で素数を生み出すことが知られています。

素数を数える

最後に，素数の個数について考えていきます。

記事の初めでは，エラトステネスの篩により，100までの自然数には素数が25個あることがわかりました。では，もっと先までの素数の個数を知りたい場合，何か方法はないのでしょうか。

素数定理

ドイツの数学者カール・フリードリヒ・ガウス（1777~1855）は15歳の頃に，10万までの自然数を一定の区間に分け，各区間に現れる素数の個数を数えている中で，素数の個数が以下の数式で表されることを予測したとされています。（15歳ｯ…!?）

ガウス自身は証明をしていませんが，100年以上後に他の数学者によって証明され，素数定理となりました。

素数定理

$x$ 以下の素数の個数 $\pi(x)$ に対して，以下のように近似できる。

$\pi(x) ～ \displaystyle \frac{x}{\log x}$

※"～"は， $x$ が十分大きいとき，両者の比が1に近づくということ。

この式を $\frac{\pi(x)}{x} ～ \frac{1}{\log x}$ と変形すれば， $x$ 近くの自然数が素数である確率は $\frac{1}{\log x}$ であると言い換えることもできそうです。

素数の出現パターンが謎であるにも関わらず，おおよその個数が高校で習う自然対数 $\log x$ と結びついているなんて，不思議ではありませんか？

素数定理 — 素数の個数が近似できる

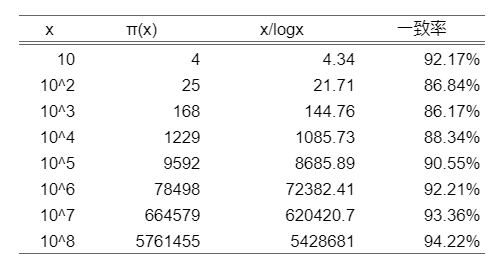
「君，1億までに素数は何個あるんだ！」と上司に脅されても，「まぁ大体これくらいです。」とは答えることができるんですね。

さらに，この式よりも精度よく素数の個数を見積もることができる，対数積分を用いた式もよく知られているので最後にご紹介します。

より精度の高い素数定理

$\pi(x) ～ \displaystyle \int_{2}^{x} \frac{dt}{\log t}$

まとめ

いかがでしたでしょうか。素数の謎は多くとも，さまざまなアプローチでその性質を知ることができるのが面白いところです。
素数には，まだまだ語り切れない程の面白い性質や不思議な現象があります。調べてみると素数の沼にはまること間違いなしです。

クイズ
オイラーの素数生成多項式 $f(n)=n^2+n+41$ において， $n=44$ とした数は素数でしょうか？

答え

$44^2+44+41=2021=43*47$
2021はいかにも素数っぽいですが，残念ながら素数ではありませんでした。
ちなみに，このように2つの素数の積で表せる整数を，半素数といいます。

参考書籍

素数物語　アイディアの饗宴中村滋著，岩波書店
ニュートン別冊数学の世界数と数式編 2020年
ニュートン別冊ゼロと無限素数と暗号 2012年