
「私の年齢は素数です。」「今日の日付は素数ですね。」など,素数に対する愛に溢れた人に出会ったことはありますか?
そういう人を見かけても,怖がったり逃げたりしないでください。それくらい,素数は人々を惹きつける性質をもった数なのです。
素数とは
まずは,素数の定義から確認しましょう。
素数(prime number)
正の約数が1と自分自身のみである自然数。ただし1は除く。
素因数分解の一意性(任意の自然数は,素数の積として順序を除いてただ一通りに表せる)のため,1は素数に含めません。
1と素数以外の自然数は素数の積で表すことができ,これを合成数といいました。それ以上分解できないという意味で,読んで字のごとく,素数は自然数の素となる数です。
素数の出現
素数が現れるタイミングは気まぐれで,規則性などはないように見えますが,それが素数の面白いところとも言えます。
ウラムの螺旋
ポーランド出身の数学者スタ二スワフ・マルチン・ウラム(1909~1984)は,整数をらせん状に並べて素数に印をつけていくと,縦横の線や斜めの線がうっすら見えることを発見しました。この模様はウラムの螺旋と呼ばれます。
ウラムは研究発表の際に,退屈しのぎに落書きをしていてこれを発見したそうです。この模様の意味は解明されていませんが,素数の出現に何らかの規則性があるかのように見えますね。

いろいろな素数
〇〇素数というように,素数はその特徴に応じて様々な名前が付けられています。ここではその一部をご紹介します。
- 双子素数:「3と5」や「11と13」のような,差が2の素数のペア
- いとこ素数:「3と7」や「7と11」のような,差が4の素数のペア
- セクシー素数:「5と11」や「7と13」のような,差が6の素数のペア
- 三つ子素数:「5と7と11」のような,(p,p+2,p+6)または(p,p+4,p+6)で表せる3つの素数の組。
これらは,素数の差に注目して分類しているものです。三つ子素数は上3つの素数を含んでいますね。
これらの素数は無数に存在すると予想されていますが,未だに証明はされていません。
メルセンヌ素数
の形で表すことのできる数を,メルセンヌ数といいます。そして,素数であるメルセンヌ数を,メルセンヌ素数といいます。
が素数であるならば,
も素数ですが,逆は成立しません。
- 例)11は素数だが,
は素数ではない。
メルセンヌ素数についても,無数に存在すると予想されていますが,証明はされていません。
現在分かっている最大の素数
素数であることが確認されている最大の数は,です(2021年4月時点)。
これは,2017年にメルセンヌ素数探索プロジェクト「GIMPS」が発見した51個目のメルセンヌ素数であり,桁数は2486万2048桁にも及びます。
これまで確認されていた最大の素数(50個目のメルセンヌ素数)よりも,約160万桁大きい数となります。
GIMPSのホームページでは,この素数が書かれたデータをダウンロードすることができます。
※なんとテキストファイルにして約24.8MB!
素数は無数に存在する
非常に大きな素数をご紹介しましたが,そもそも素数に”最大値”はあるのでしょうか?
答えはNoです。実は,素数が無数に存在することは古代ギリシャから知られていました。この証明はユークリッドの『原論』に記されています。
簡潔な証明ですので,少し見てみましょう。
任意の異なる個の素数をとり,そのリストを
とおく。
という数を考える。
はリストにあるどの素数でも割っても1余るので割り切れない。
したがってはリストにない新しい素数であるか,リストにない別の素数で割り切れなければならない。
よって新たな素数が存在する。
これを繰り返すと次々と新しい素数がみつかるので,素数は無限に存在する。
他にも背理法を使った方法などが有名ですが,フィリップ・サイダックは次のような証明を与えました。
を1より大きい任意の整数とする。
と
は互いに素より,
は少なくとも2つの異なる素因数をもつ。
同様に,は少なくとも3つの異なる素因数をもつ。
これを繰り返すと,いくらでも多くの異なる素因数をもつ数を生成できるので,素数は無限に存在する。
連続する2つの自然数は互いに素であることを用いた,非常にエレガントな証明ですが,なんとこの証明が発表されたのは2006年だそうです。
こんなにシンプルな証明が,つい最近まで見出されなかったというのは驚きですね。もしかすると,まだまだ証明方法はあるのかもしれません。
まとめ
素数については未だに謎が多く,不思議な現象を見せるからこそ,魅力的なのかもしれません。後編では,素数の出現や個数など,より詳しい内容に踏み込む予定です。
最後にもう一つ,こちらの画像をご覧ください。
これは517桁の素数を11行×47列に並べ,1だけ色を変えたものです。何か文字が浮かび上がって見えませんか…?
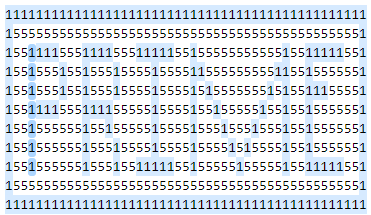
参考書籍・サイト
- 素数物語 アイディアの饗宴 中村 滋著,岩波書店,2019年
- ニュートン別冊 数学の世界 数と数式編 2020年
- ニュートン別冊 ゼロと無限 素数と暗号 2012年
- Prime Curios!(素数に関する面白い雑学がまとめられています)

